定义
脉冲时域上的光强形状为抛物线形的脉冲。
抛物线型脉冲的光脉冲(通常的超短脉冲)在时域上其光强不仅仅在邻近脉冲中心的地方具有抛物线的形状,而且在脉冲边缘光强接近于零的地方也符合抛物线的形状。在理想的情况下,该脉冲的光强分布如下所示:
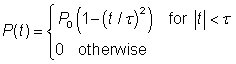
图1给出了一个近似抛物线型的脉冲,这种脉冲可以通过一定情况下的光纤放大器产生。抛物线型脉冲具有一些特殊的性能,这些性能对于在光纤放大器的产生高能量的超短脉冲是尤其重要的。
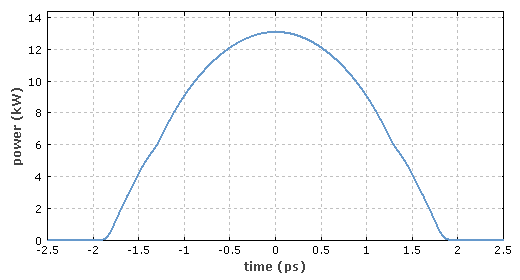
图 1 近抛物线型脉冲的时域分布,其可以通过在光纤放大器中放大一个高斯型脉冲产生。
上啁啾的抛物线型脉冲可以利用光纤放大器产生,脉冲在其中不仅仅经历光学增益,同时还受到克尔非线性和正常色散的作用。在这种情况下,具有啁啾的抛物线型脉冲是长传播长度长度下[3,8]的渐近解。在具有足够大的放大系数的情况下,经过足够长的光纤传播后,将所得的脉冲的形状将不再依赖于种子脉冲的形状或脉宽,而峰值功率和脉宽在经过很擦汗那个的传播长度之后只依赖于种子脉冲的能量。这就是自相似的脉冲传播情况,在这种情况下,虽然脉冲的脉宽发生了变化,但抛物线型脉冲的形状并不会发生改变。因此,这种脉冲有时被称为自相似子(similaritons)。脉冲脉宽为:
![]()
其中g是指数下的增益系数,其全带宽(不是半高全宽)为:

两者均随着脉冲能量Ep的立方根增长,使得脉冲的时间带宽积随着EP2/3增长。
该脉冲具有一个接近线性的上啁啾,即一个线性上升的瞬时频率,而瞬时频率的增长速率是与脉冲能量无关的:
![]()
随着传播长度的增长,峰值功率随EP2/3成比例的上升。啁啾率(以Hz/ ps为单位)接近与恒定值,仅由光纤色散和单位长度的增益决定的。谱宽则正比于脉冲持续时间,或者说随EP1/3成比例上升。
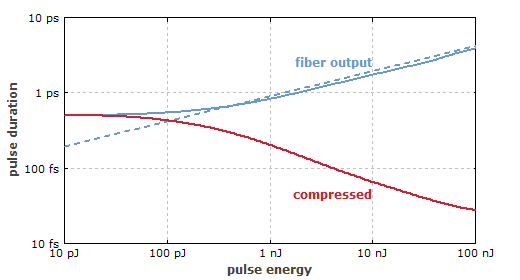
图 2 脉冲脉宽在一个具有无限增益带宽的放大器中的演化过程。蓝色和红色实线分别给出了脉冲持续时间在所述放大器和压缩器后的脉冲宽度。虚线则给出了渐近值,在这种情况下,放大倍率约为20dB。
受输入脉冲参数的限制,特别是脉冲脉宽和能量的限制,抛物线演化过程只会在一定量的线性增长后发生。因此,即使在脉冲能量增加了几个数量级,脉冲脉宽和带宽也不一定上升几个数量级。如图2所示,其所述的种子脉冲能量为10个pJ,脉宽为500 fs。最初,所述的放大是几乎线性的,但随后带宽和脉宽都开始显著上升。由于带宽的增加,导致压缩后脉冲比初始脉冲更短。
需要注意的是一个实际中的光纤放大器的有限增益带宽限制了抛物线型脉冲放大过程的脉冲能量。而图2中的参数,就已经远远超出了这一限制。
抛物线型脉冲放大的亮点
抛物线型脉冲的特性导致了当光纤放大器被设计为“抛物线型放大器时”时具有了对超短脉冲的放大的诸多吸引人的特性:
1、避免了脉冲分裂。放大所产生的脉冲在时域和频域上都不具有显著的旁瓣。
2、这种放大器中种子源并不需要精确设计的脉冲参数。只要该放大器的放大系数足够大,这些参数就都不重要。种子脉冲的脉宽可以比输出脉冲的脉宽宽很多。但是脉宽也不应该太长,否则作为渐近解的抛物线型脉冲需要很长的过程才能达到。
3、光纤参数(色散,非线性和增益)也不是非常严格的。
4、由于放大后的脉冲是具有近似线性啁啾的,它是比较容易就能通过脉冲压缩获得接近变换极限脉冲的。但是,压缩器的高阶色散不宜过多。
5、放大期间的啁啾是有益的因素,因为对变换极限脉冲的放大可能导致过度的非线性相移。这种情况类似与啁啾脉冲放大,但脉冲的展宽量较小。
这种放大的限制来自以下作用:
1、有限的增益带宽限制了可能的脉冲能量。对于标准的模场面积的掺镱光纤,其能量只在数十nJ,远低于饱和能量。因此,抛物线型脉冲只能提取光纤所存储能量的一小部分。这一作用使得这样的放大器适合于具有非常高的重复频率,但脉冲能量并不十分大的情况。
2、原则上,被放大的脉冲会在较长的波长产生较高的拉曼增益,从而产生一个较强的斯托克斯脉冲,导致原来的脉冲被扭曲。但是,抛物线型脉冲放大器通常不会产生那么搞的拉曼增益。
3、光纤和压缩器的较高阶色散不应太强。
4、放大器噪声在某些情况下也会限制放大器的能量。
最好通过数值模拟脉冲放大的传播过程来获得最佳的放大器设计。
抛物线型脉冲放大的原理也适用于锁模光纤激光器[6](自相似光纤激光器)。在这种情况下,循环传播脉冲的光谱宽度是强烈振荡:放大期间它会增加,通过一些光滤波器来重置每个循环。这种方法使得有可能通过廉价的光纤激光器来获得较高的脉冲能量。
参考文献
[1] D. Anderson et al., “Wave-breaking-free pulses in nonlinear-optical fibers”, J. Opt. Soc. Am. B 10 (7), 1185 (1993)
[2] K. Tamura and M. Nakazawa, “Pulse compression by nonlinear pulse evolution with reduced optical wave breaking in erbium-doped fiber amplifiers”, Opt. Lett. 21 (1), 68 (1996)
[3] M. E. Fermann et al., “Self-similar propagation and amplification of parabolic pulses in optical fibers”, Phys. Rev. Lett. 84 (26), 6010 (2000)
[4] V. I. Kruglov et al., “Self-similar propagation of high-power parabolic pulses in optical fiber amplifiers”, Opt. Lett. 25 (24), 1753 (2000)
[5] T. Hirooka and M. Nakazawa, “Parabolic pulse generation by use of a dispersion-decreasing fiber with normal group-velocity dispersion”, Opt. Express 29 (5), 498 (2004)
[6] F. Ö. Ilday et al., “Self-similar evolution of parabolic pulses in a laser”, Phys. Rev. Lett. 92 (21), 213902 (2004)
[7] C. K. Nielsen et al., “Self-starting self-similar all-polarization maintaining Yb-doped fiber laser”, Opt. Express 13 (23), 9346 (2005)
[8] V. I. Kruglov and J. D. Harvey, “Asymptotically exact parabolic solutions of the generalized nonlinear Schrödinger equation with varying parameters”, J. Opt. Soc. Am. B 23 (12), 2541 (2006)
[9] T. Schreiber et al., “Microjoule-level all-polarization-maintaining femtosecond fiber source”, Opt. Lett. 31 (5), 574 (2006)
[10] A. Ruehl et al., “Dynamics of parabolic pulses in an ultrafast fiber laser”, Opt. Lett. 31 (18), 2734 (2006)
[11] J. M. Dudley et al., “Self-similarity and scaling phenomena in nonlinear ultrafast optics”, Nature Phys. 3, 597 (2007)
[12] D. N. Papadopoulos et al., “Generation of 63 fs 4.1 MW peak power pulses from a parabolic fiber amplifier operated beyond the gain bandwidth limit”, Opt. Lett. 23 (17), 2520 (2007)
[13] R. Paschotta, case study on parabolic pulses in an ytterbium-doped fiber amplifier
[14] R. Paschotta, tutorial on "Fiber Amplifiers", part 8 on ultrafast amplifiers
参阅:光纤放大器、非线性、啁啾脉冲放大、脉冲压缩



