在1946年，Bloch提出了一个微分方程来衡量在外磁场
的影响下，核磁化强度随时间的变化
：
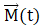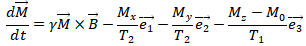
其中，γ是核的旋磁比，T1和T2分别为纵向弛豫时间和横向弛豫时间。
当不存在弛豫时，Bloch方程可以简化为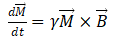
，为外磁场 中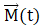 的lamor进动方程。
在旋转坐标系中，假设不存在弛豫，在t=0时，横向磁化Mxy (0)受到恒定磁场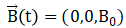
的作用，且B0为正，则Bloch方程可以简化为两个互相不耦合的线性微分方程：
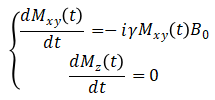
方程的解为：
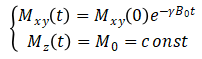
由此可见，横向磁化Mxy绕z轴以角频率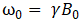
顺时针旋转，纵向磁化Mz随时间保持为一个常数。得到横向磁化Mxy (t)后，Mx (t)和My (t)也可以相应得出：
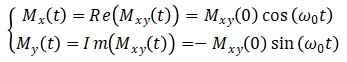
其中，Re和Im分别表示取复数的实部和虚部，且在以上计算过程中，需要假设Mxy (0)为一个实数。
参考文献
[1] Pule J V. The Bloch equations[J]. Communications in Mathematical Physics, 1974, 38(3): 241-256.
[2] https://en.wikipedia.org/wiki/Bloch_equations
