定义
假设A为m×n的矩阵，A的奇异值分解为
，其中，U为m×m的正交矩阵，V为n×n的正交矩阵，
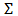为非负的m×n对角阵，其主对角元
，称为矩阵A的奇异值。
特种值与特征向量
奇异值分解SVD是方阵特征值分解在任意矩阵上的推广。我们要回顾方阵的特征值分解，首先认识一些概念：特征值与特征向量。
如果一个n维向量x与n×n实对称矩阵B的可以写成：Bx=λx，则λ是方阵B的一个特征值，而x是特征值λ所对应的特征向量。
例1：实对称矩阵的特征值和特征向量
对于矩阵
，有
，或
；则3是B的一个特征值，其对应的特征向量是
，2也是B的一个特征值，其对应的一个特征向量是
；
实对称矩阵的特征值分解eigenvalue decomposition（EVD）：
式中矩阵维度都是n×n，Q是标准正交阵，QTQ=I，Q中的列向量称为特征向量qi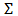， 是对角矩阵，其对角元素是与特征向量qi对应的特征值λi。
例2：实对称矩阵的特征值分解
实对称矩阵
。
特征向量之间两两正交，互不相关，可视作一组基向量，而特征值则表示矩阵B在相应基方向上的取向/缩放程度。
从特征值分解到奇异值分解
特征值分解要求矩阵为方阵，而现实问题中遇到的常常是行列不等的矩阵，该如何分解呢？回顾 SVD定义：
U和V都是单位正交阵（其中的向量两两正交，每个向量的模值为1），满足UTU=I， VTV=I，其中U称为左奇异矩阵，V称为右奇异矩阵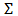，仅在主对角线上有值，称为奇异值。上式矩阵维度分别为
，SVD分解图示如下：
图 1 SVD分解示意图
SVD与EVD有什么联系呢？这里的奇异值
与λi 特征值又是什么关系呢？
将矩阵A转换为方阵，有
与
两种形式，AAT通过EVD得到的特征向量组成的矩阵即为SVD中的左奇异矩阵U，而AAT通过EVD得到的特征向量组成的矩阵即为SVD中的右奇异矩阵V，以V矩阵证明为例：
同样可得特征值矩阵等于奇异值矩阵的平方，
奇异值分解的几何解释与应用
一个矩阵一个看作是一个线性变换，而SVD变换，就是将这个复杂的变换分解为三个简单得基本变换，从而使这个变换体现除了更本质的信息，是一种广义的特征值分解。
对于特征值分解
，理解为B是处于Q中所有特征向量（一组正交基）构成的空间中，而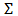中的特征值表示各个基底上的取向/缩放程度；从几何变换的角度来看矩阵B，它所代表的变换本质上是在原n维空间中各个基底方向上进行缩放。
对于奇异值分解
，从几何变换的角度来看矩阵A，可以看作三个连续的变换VT、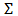、U，依次为旋转、缩放、旋转（正交矩阵的作用都是旋转矩阵）。V中的所有列向量是n维空间的一组正交基，而U中的所有列向量是m维空间的一组正交基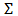，中奇异值的大小代表了n维空间中基向量映射到m维空间中相应基方向上的缩放程度，也代表了这两空间中相应基向量的差异程度，因此若奇异值越大，则此奇异值对最后空间的影响越大。
图 2 奇异值分解将矩阵A代表的复杂变换分成三步变换
一个矩阵的分解结果是不唯一的，在SVD中，规定了奇异值从大到小排列，从而唯一确定了一种分解结果；在很多情况下，奇异值下降得特别快，前10%甚至1%的奇异值之和就占据了全部奇异值和的99%以上，因此可以只使用前k个显著的奇异值与对应的左右奇异向量即可近似描述原矩阵：
基于此，SVD可用于PCA降维，进行数据压缩与图像去噪；也可用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。
参考文献
[1] Wall, M. E., Rechtsteiner, A., & Rocha, L. M. (2003). Singular value decomposition and principal component analysis. In A practical approach to microarray data analysis (pp. 91-109). Springer, Boston, MA.
[2] Austin, D. (2017). We recommend a singular value decomposition. American Mathematical Society (AMS). Retrieved June, 20.
[3] https://www.zhihu.com/question/22237507
[4] https://zhuanlan.zhihu.com/p/59324612
参阅：特征值分解、PCA、奇异值分解、SVD、EVD、特征提取
