概述
在统计,缩放的相关是系数的形式的相关性适用于具有时间分量,例如数据的时间序列。这是平均短期相关性。如果信号具有多个分量(慢速和快速),则可以仅针对信号的快速分量计算缩放的相关系数,而忽略慢速分量的贡献[1] 。这种类似于滤波的操作的优点是不必对信号的正弦性质进行假设。
例如,在脑信号研究中,研究人员通常对高频分量(β和γ范围; 25–80 Hz)感兴趣,而对低频范围(α,θ等)则不感兴趣。在那种情况下,只能通过选择分析标度s,以对应于该频率的周期(例如, 对于25 Hz振荡,s = 40 ms),才能对高于25 Hz的频率计算比例相关。
定义
两个信号之间的比例相关性定义为在这些信号的短段之间计算出的平均相关性。首先,有必要确定段数K可以适合信号的总长度T 给定比例 s:

接下来,如果rk是k段的皮尔逊相关系数,那么整个信号的比例相关![]() 表示为:
表示为:
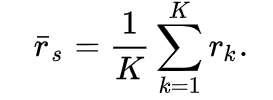
效率
在详细分析中,Nikolić等人[1]表明,慢速分量贡献的衰减程度取决于三个因素,比例的选择,慢速分量和快速分量之间的振幅比以及其振荡频率的差异。振荡频率的差异越大,从计算出的相关系数中去除慢速成分的贡献就越有效。类似地,慢速成分相对于快速成分的功效越小,按比例缩放的相关性能越好。
优点
在许多情况下,比例相关应优于基于频谱方法的信号滤波。比例相关的优点在于,它不会对信号的频谱特性(例如,信号的正弦形状)做出假设。Nikolić等[1]表明,使用维纳-欣钦定理去除慢速分量不及通过比例相关获得的结果。这些优势尤其明显,尤其是在信号不是周期性的信号或由离散事件(例如已检测到神经元动作电位的时间戳)组成的情况下。
参考文献
[1] Nikolić D, Mureşan R C, Feng W, et al. Scaled correlation analysis: a better way to compute a cross‐correlogram[J]. European Journal of Neuroscience, 2012, 35(5): 742-762.
参阅:互相关



