滤波的目标在于,尽可能将含噪信号中的噪声去除,具体来说,已知一个含噪信号x=s+v,我们希望设计一个滤波器h,使得信号x经过滤波器之后,得到信号![]() ,并使得输出
,并使得输出![]() 尽可能接近原始信号s。即:
尽可能接近原始信号s。即:
![]()
在离散域内上式中对h求导,得到:
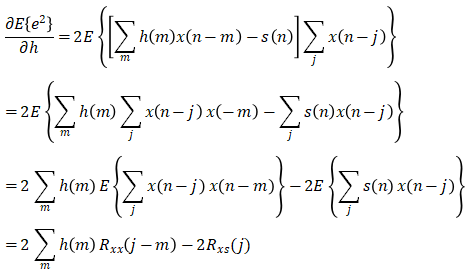
令导数为零得到:
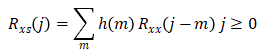
以上方程就是维纳霍夫方程,求解维纳霍夫方程可以帮助进行滤波器的设计。然而,维纳霍夫方程的精确求解并不容易,往往需要依赖一些近似的方法,以下通过两类维纳滤波器(传统维纳滤波器和参数维纳滤波器)进行举例。
在希望针对图片I进行滤波时,存在传统维纳滤波器和参数维纳滤波器,在以下的例子中,F代表滤波器,图片中无噪声部分为St,噪声为![]() ,通过滤波器得到的估计信号为S,即存在以下关系:
,通过滤波器得到的估计信号为S,即存在以下关系:
![]()
传统维纳滤波器
传统维纳滤波器通过将以下表达式中的W最小化而得到:
![]()
此外,需要对噪声进行假设,假设信号和噪声不相关,基于这一假设,可以得到滤波器的近似解为:
![]()
其中,Se是信号的一个估计,一般可以通过以下方法获得:
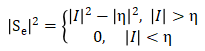
这里需要注意,由于|F|<1,一般不会将经过滤波后的数据再次迭代进行滤波。
参数维纳滤波器
滤波的目前在于将图片与信号之间的差异尽可能缩小,参数维纳滤波器引入S和λ,将以下表达式中的W最小化:
![]()
其中,Q是某个作用于信号上的线性运算符,λ是拉格朗日乘子,同样假设信号和噪声之间不相关,通过最大化信号与噪声之间的比值的方法,可以得到如下形式的近似解:
![]()
当λ取1时,参数维纳滤波器与传统维纳滤波器相同。
参考文献
[1] Marks, L. D. Wiener-Filter Enhancement of Noisy HREM Images. Ultramicroscopy 1996, 62 (1–2), 43–52.
[2] https://doi.org/10.1016/0304-3991(95)00085-2.



