定义
是一种统计(降维)方法。在数据满足正态分布的前提下,设法将原来众多具有一定相关性的高维数据,重新组合成一组新的互相无关的特征向量和特征值来代替原来的指标。
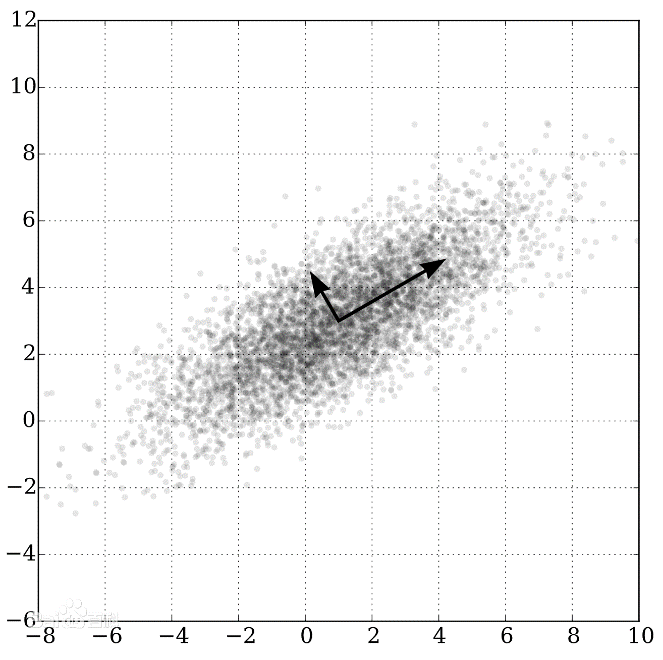
图 1 PCA示意图(将具有相关性的二维数据转化为两个正交的特征向量&特征值)
背景
主成分分析由卡尔·皮尔逊于1901年发明,用于分析数据及建立数理模型。其方法主要是通过对协方差矩阵进行特征分解,以得出数据的主成分(即特征向量)与它们的权值(即特征值)。PCA是最简单的以特征量分析多元统计分布的方法。其结果可以理解为对原数据中的方差做出解释:哪一个方向上的数据值对方差的影响最大?换而言之,PCA提供了一种降低数据维度的有效办法;如果分析者在原数据中除掉最小的特征值所对应的成分,那么所得的低维度数据必定是最优化的(也即,这样降低维度必定是失去讯息最少的方法)。主成分分析在分析复杂数据时尤为有用,比如人脸识别。
思想:最大的保留原有数据的样子,通过分解为正交的特征向量。
不求推导,通过图像来理解:
一般来说,二维的样本点在坐标图中任意一条向量上都可以投影成一维的,那么我们如何选择最佳投影向量呢?我们提到需要在最大程度上保留数据集的信息量的前提下进行数据维度的降低,因此我们需要有优化目标来对图中的向量进行选择。
而PCA的优化目标就是:
(1)对于 2 维降到 1 维:找到一个投影方向,使得投影误差和最小。
(2)对于 n 维降到 k 维:找到 k 个向量定义的 k 维投影平面,使得投影误差和最小。
那么投影误差又是什么呢?投影误差即为,每一个样本点到投影向量或者投影平面的距离。而投影误差和即为所有样本点到投影向量或投影平面的距离的和。
为什么要将“投影误差和最小”最为优化目标呢?
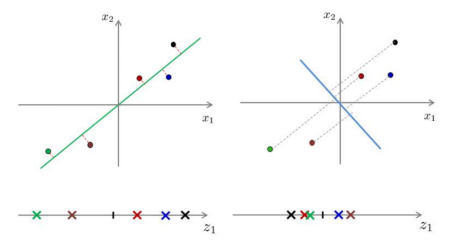
图 2 投影误差最小(左图)&投影误差最大(右图)
我们以以下例子进行解释。下面两幅图展示了两种不同投影向量:
我们能够和清楚地看到,对于第一种向量的投影误差和一定比第二种的投影误差和要小。
假设对于原样本中,位于第一象限的三个样本点属于类别“A”,位于第三象限的两个样本点属于类别“B”。经过投影后,我们可以看出,对于第一种降维,在降维后仍旧保持了位于原点右侧的三个样本属于类别“A”,位于原点左侧的两个样本属于类别“B”。而对于第二种投影,明显可以看出,已经不能够分辨出样本的类别了。换句话说,第二种投影方式丢失了一些信息。
因此,“投影误差和最小”便成为我们所需要优化的目标。
那么如何寻找投影误差最小的方向呢?
寻找到方差最大的方向即可。方差最大与投影误差最小这两个优化目标其实本质上是一样的。
PCA家族分类

图 3 PCA及其衍生算法总结
参考文献
[1] Wold S, Esbensen K, Geladi P. Principal component analysis[J]. Chemometrics and intelligent laboratory systems, 1987, 2(1-3): 37-52.
[2] https://www.imooc.com/article/details/id/31164
参阅:正态分布、协方差矩阵、Kernel PCA、Nonlocal PCA、Robust PCA、Sparse PCA、PCA工具包安装及其使用



