定义
自举这个概念,在计算机领域和统计领域均有出现,这里我们对统计领域中的自举法进行说明。
自举法是重抽样方法的一种,由Bradley Efron于1979年在《Annals of Statistics》上首次发表[1]。该方法从给定训练集中有放回的均匀抽样,也就是说,每当选中一个样本,它等可能地被再次选中并被再次添加到训练集中。在假设一组观测数据来自独立同分布的总体的情况下,可以通过多次抽样得到与观测数据集大小相同的集合,来替代观测数据集。自举法无需对总体进行任何假设检验,当参数模式假设难以获得,且无法进行参数推断时,自举法多被用来替代基于参数模型假设的统计推断。
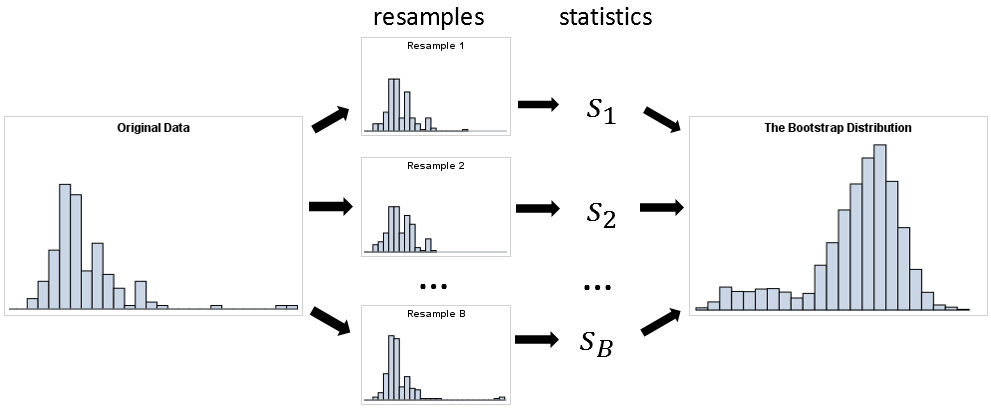
图 1 自举法重采样示意图[3]
优点
bootstrap的一大优点是简单。对于复杂参数的分布估计器,例如百分比点、比例和相关系数,它是一种直接的方法来获得标准误差和置信区间的估计。对于大多数问题,不可能知道真实的置信区间,但bootstrap渐进地比使用样本方差和正态性假设得到的标准区间更精确。bootstrapping也是一种方便的方法,它避免了重复实验获取其他组样本数据的成本。
缺点
自举法的结果可能取决于部分有代表性的样本。
参考文献
[1] Efron, B. (1979). "Bootstrap methods: Another look at the jackknife". The Annals of Statistics. 7 (1): 1–26. doi:10.1214/aos/1176344552
[2] wiki: https://en.wikipedia.org/wiki/Bootstrapping_(statistics)#cite_note-4
[3] https://blogs.sas.com/content/iml/2018/12/12/essential-guide-bootstrapping-sas.html



