定义
循环排列是指在一个圆环上等距离放置n个不同的物体,使这些物体相邻关系不一样的所有排列方式的组合。也就是说,这个圆环可以朝一个方向任意旋转,但是这些排列关系都不会重复。
示例[1]
下图展示了n=3的情况,该情况下循环排列有两种,分别是 {1,2,3} 和 {1,3,2}。
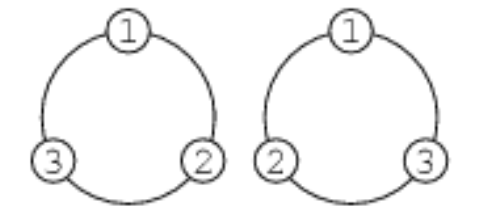
下图展示了n=4的情况,共有六种循环排列方式。

理论个数
当只允许朝一个方向旋转时,也就是上述情况下,n个物体的循环排列个数为(n-1)!
也有的循环排列认为逆时针和顺时针旋转等效,此时n个物体的循环排列个数为1/2(n-1)!
实际应用
在进行神经元荧光信号和小鼠行为的相关性分析时,我们需要确定当前神经元的亮、灭变化是否特异地和某个小鼠行为对应时,可以产生一些随机的神经元信号,计算这些随机信号与行为的相关程度,并与原始信号进行对比。这里,如果针对时间点进行随机打乱的话,很容易破坏掉信号中的连续事件(譬如钙瞬变事件)。
为了在随机打乱时,保留这些完整的信号事件,可以采取循环排列的思想,在信号中随机选取一个时间点t,t以前的信号和t以后的信号被认为是两个元素 {1} 和 {2},这样,原始信号为 {1,2},打乱后的信号是 {2,1},这样的优点在于:只改变了事件和时间的对应关系,而没有破坏事件本身的连续性。
参考文献
[1] Weisstein, Eric W. "Circular Permutation." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/CircularPermutation.html



