定义
形态学,即数学形态学(Mathematical Morphology),是基于集合论的图像(形状)分析和处理的理论框架。通过将结构元素作用于输入图像,使得输出的图像可以简化图像数据,保留对象的基本形状特征,并可以消除不相关的对象。
形态学操作技术最初是由巴黎矿业大学的Matheron和Serra [1]开发的。最初,它仅适用于二进制图像,但随后也被扩展到灰度图像和彩色图像中。
数学形态学中最基本的两个操作是 腐蚀(移除小物体并使通过小桥连接的物体断开连接)和膨胀(填充孔并平滑轮廓线)。这两个运算都将两条数据作为输入:要腐蚀或膨胀的原始图像,以及结构元素(也称为内核,Kernel)。在二值图像学中,结构元素为一个二值的小图像块儿,作为分析影像时使用的“刷子”,代表当处理影像上的某点时、要取出周围的哪些点进行运算[2] 。图1显示了许多不同大小的不同结构元素。最常见的类型是适合于以其原点为中心的3×3网格的结构元素。
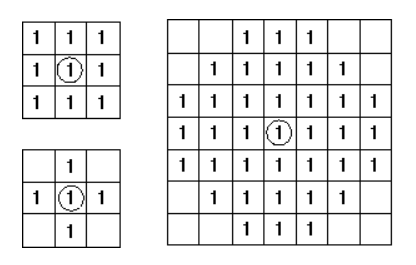
图 1 一些示例的结构元素
腐蚀
如下图所示,把结构元素B平移a后得到Ba,若Ba包含于X,我们记下这个a点,所有满足上述条件的a点组成的集合称做X被B腐蚀(Erosion)的结果。其中X是被处理的对象,B是结构元素,结构元件B在本示例中是圆盘,但是它可以是任何形状。对于任意一个在阴影部分的点a,Ba 包含于X,所以X被B腐蚀的结果就是那个阴影部分。阴影部分在X的范围之内,且比X小,就象X被剥掉了一层似的。
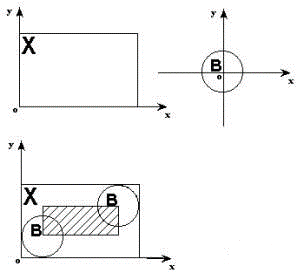
图 2 腐蚀示意图[3]
膨胀
膨胀(dilation)可以看做是腐蚀的对偶运算,其定义是:把结构元素B平移a后得到Ba,若Ba击中X,我们记下这个a点。所有满足上述条件的a点组成的集合称做X被B膨胀的结果。如下图所示。

图 3 膨胀示意图[3]
进一步的,腐蚀和膨胀可以多种方式并行和串联使用,以进行其他转化,最典型的例子是开运算和闭运算。其中开运算是先腐蚀后膨胀,而闭运算是先膨胀后腐蚀。一般来说,开运算可以使图像的轮廓变得光滑, 还能使狭窄的连接断开和消除细毛刺。如图4所示,开运算断开了团中两个小区域间一个像素宽的连接(断开了狭窄连接),并且去除了右侧物体上部突出的一个小区域(消除细毛刺)。但与腐蚀不同的是,图像大的轮廓并没有发生整体的收缩,物体位置也没有发生任何变化。
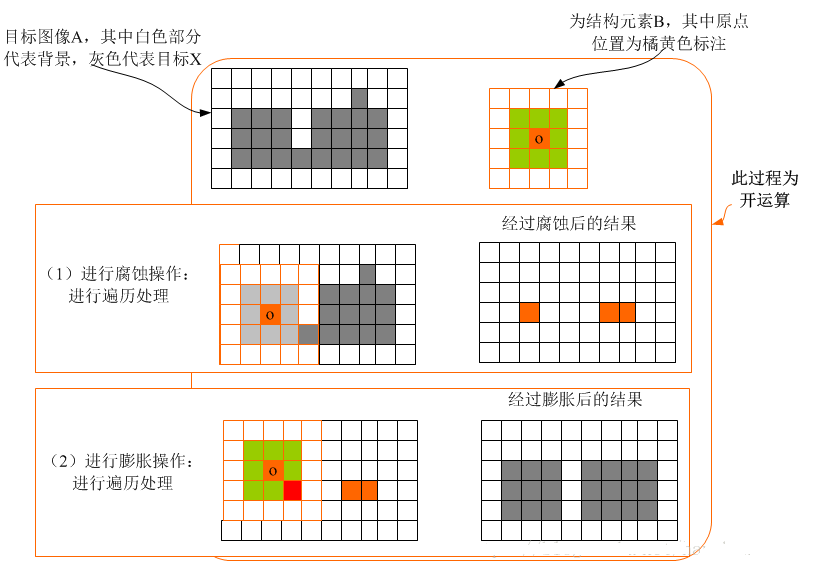
图 4 开运算示意图[3]
闭运算同样可以使轮廓变得光滑, 但与开运算相反, 它通常能够弥合狭窄的间断, 填充小的孔洞。
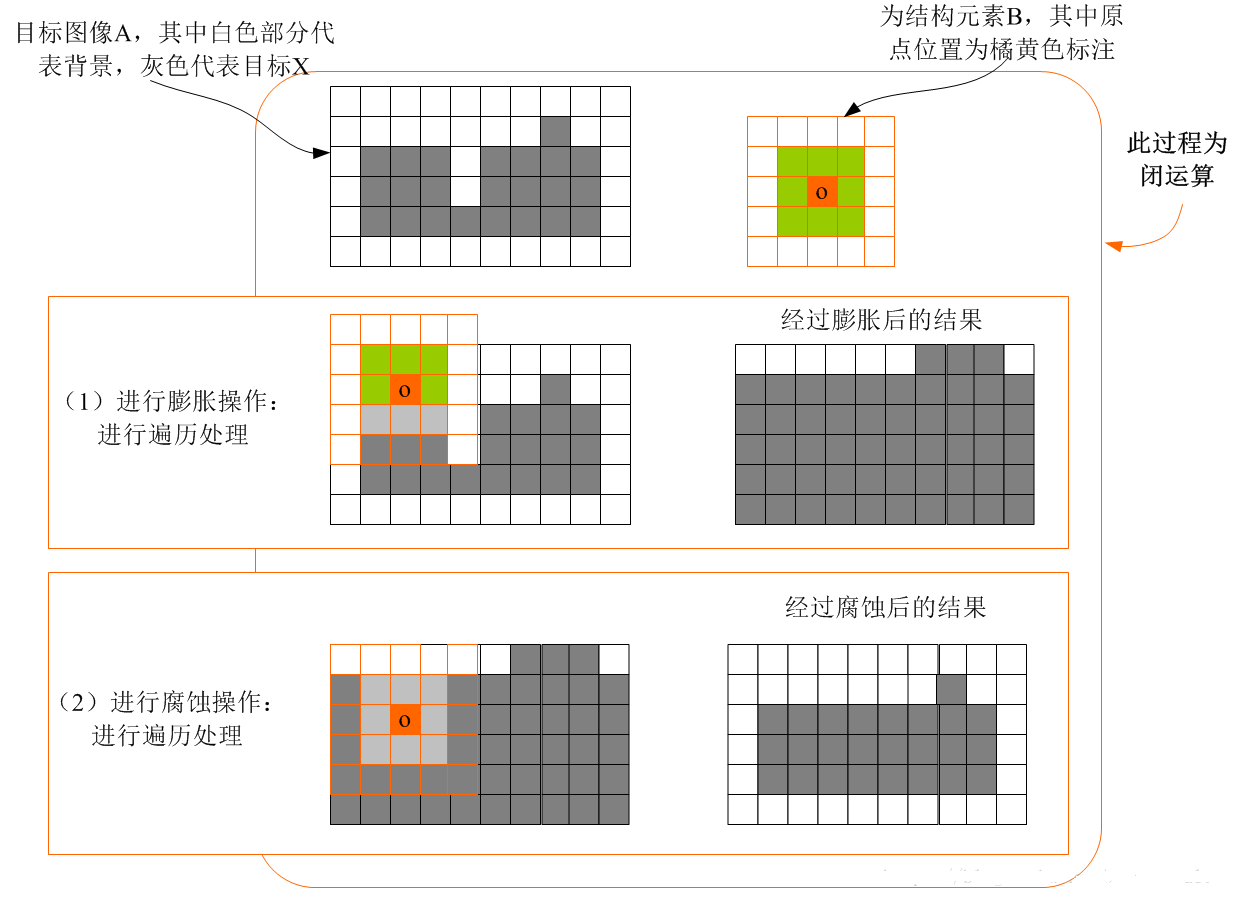
图 5 闭运算示意图[3]
参考文献
[1] J. Serra. Image Analysis and Mathematical Morphology. Academic Press, 1982.
[2] https://homepages.inf.ed.ac.uk/rbf/HIPR2/strctel.htm
[3] https://zhuanlan.zhihu.com/p/46305029
[4] https://blog.csdn.net/caojinpei123/article/details/81916005



