定义
中心切片定理是指,密度函数f(x,y)在某一方向上的投影函数R(s,α)的一维傅里叶变换,是密度函数f(x,y)的傅里叶F(kx,ky)变换在(s,α)平面上沿着同一方向过原点直线上的值。
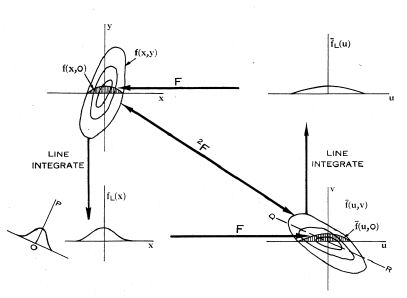
图 1 中心切片定理
中心切片定理是CT图像重建的基本定理,保证了投影和频域轮廓线之间的傅里叶关系。
中心切片定理的证明
Radon变换是指,密度函数f(x,y) 在某一方向上的投影,数学表达为:
![]()
其对于S的一维傅里叶变换为:

而密度函数f(x,y)的傅里叶变换为:
![]()
考虑在α 方向上,

那么可以看出:
![]()
定理得证。
中心切片定理的应用
1、射电望远镜图像重建
1956-1958年,Ronald N. Bracewell提出了射电干涉测量和主流重建方法,其中包含基于中心切片定理的算法。
在射电望远镜中,条带积分指使用一个具有长而窄的孔径的射电望远镜接收来自狭长天空的辐射(接收到的是L上所有射电强度的积分),对于中心切片定理中,即为密度函数f(x,y) 在某一方向上的投影函数R(s,α) 。

图 2 射电望远镜中的中心切片定理
首先,保持θ不变,通过地球的自传或者调整天线的转变实现R的遍历;随后改变θ,再实现R的变换,即可实现二维傅里叶变换的填充。从而根据中心切片定理,通过二维傅里叶变换,即可重建出到射电望远镜的图像[1,2] 。
正是中心切片定理在射电望远镜中的应用,启发了后来的CT重建思想。
2、CT图像重建
在CT成像中,探测器接收到的是射线源穿过人体之后的射线。由于发射和接收处的射线能量的衰减即为射线穿过的人体组织对于射线吸收系数的条带积分,对应于中心切片定理中的投影函数R(s,α) 。通过改变射线源发射和探测器接收的角度,可以在(s,α) 平面中遍历密度函数f(x,y) 。
根据中心切片定理,只需将探测器接收到的R(s,α) 做傅里叶变换,再在(s,α) 方向中做二维傅里叶逆变换,即可得到重建后的CT图像。
3、PET图像重建
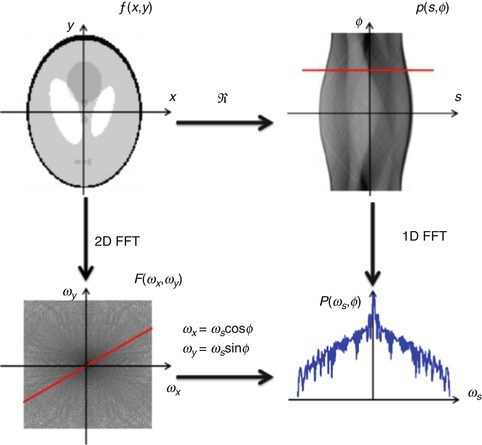
图 3 PET的中心切片定理[3]
在PET成像中,探测器接收到的是体内发出正电子信号,探测器接收的是同一个方向上的正电子信号密度函数f(x,y) 的积分值,对应于中心切片定理中的投影函数R(s,α) 。通过改变各个接收器的接收角度,即可实现(s,α) 平面中的遍历。
根据中心切片定理,只需将探测器接收到的R(s,α) 做傅里叶变换,再在(s,α) 方向中做二维傅里叶逆变换,即可得到重建后的PET图像。
参考文献
[1] Bracewell R N. Strip integration in radio astronomy[J]. Australian Journal of Physics, 1956.
[2] Bracewell R N, Riddle A C. Inversion of fan-beam scans in radio astronomy[J]. The Astrophysical Journal, 1967, 150: 427.
[3] https://radiologykey.com/pet-image-reconstruction-methodology-and-quantitative-accuracy/
参阅:CT重建、Radon变换



