定义
泊松噪声,或称散粒噪声,是一种可以通过泊松过程建模的噪声。在电子学中,泊松噪声是由于离散电荷的性质造成的。泊松噪声也会在光学设备对光子计数时产生,这和光子的不确定性有关[1]。

(图片源于网络)
成因
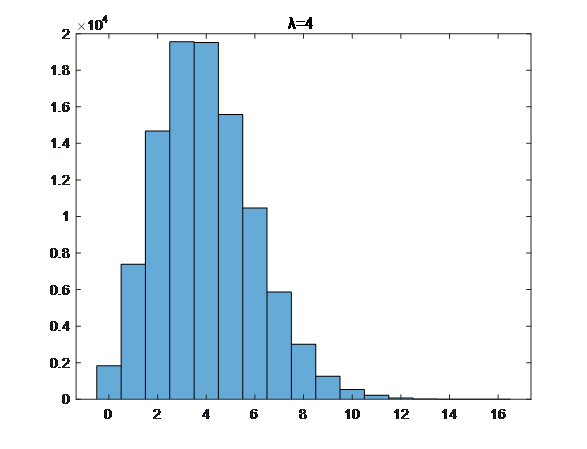
存在的根本原因是因为光是由离散的光子构成(光的粒子性)。光源发出的光子打在CMOS上,从而形成一个可见的光点。光源每秒发射的光子到达CMOS的越多,则该像素的灰度值越大。但是因为光源发射和CMOS接收之间都有可能存在一些因素导致单个光子并没有被CMOS接收到或者某一时间段内发射的光子特别多,所以这就导致了灰度值会有波动,也就是所谓的散粒噪声。举例而言,在光源强度比较低的时候,比如说设定光强为每秒5个光子的时候,那么每秒实际CMOS接受到的光子数可能从0到10(服从泊松分布)。
和泊松分布的关系
从成因中不难看出,泊松噪声是一种和光强相关的噪声,光强越大,接收到的光子数波动越大,因此泊松噪声越严重。泊松分布是一种均值等于方差的分布,因此可以很好地形容“越亮则波动越大”这一现象,因此采用泊松分布来建模:
![]()
其中数学期望![]() ,方差
,方差![]() 。
。
消除方式
常见的消除方式是首先通过方差稳定变换,将原始图像或视频转换为方差稳定的图像或视频,假设在图像或视频的局部区域均值保持稳定,则可以使用诸如 Nonlocal-means 等方法进行去除,然后逆变换得到去噪后的图像。常用于光学成像泊松噪声去除的方法为 Anscombe 变换[2],即:
![]()
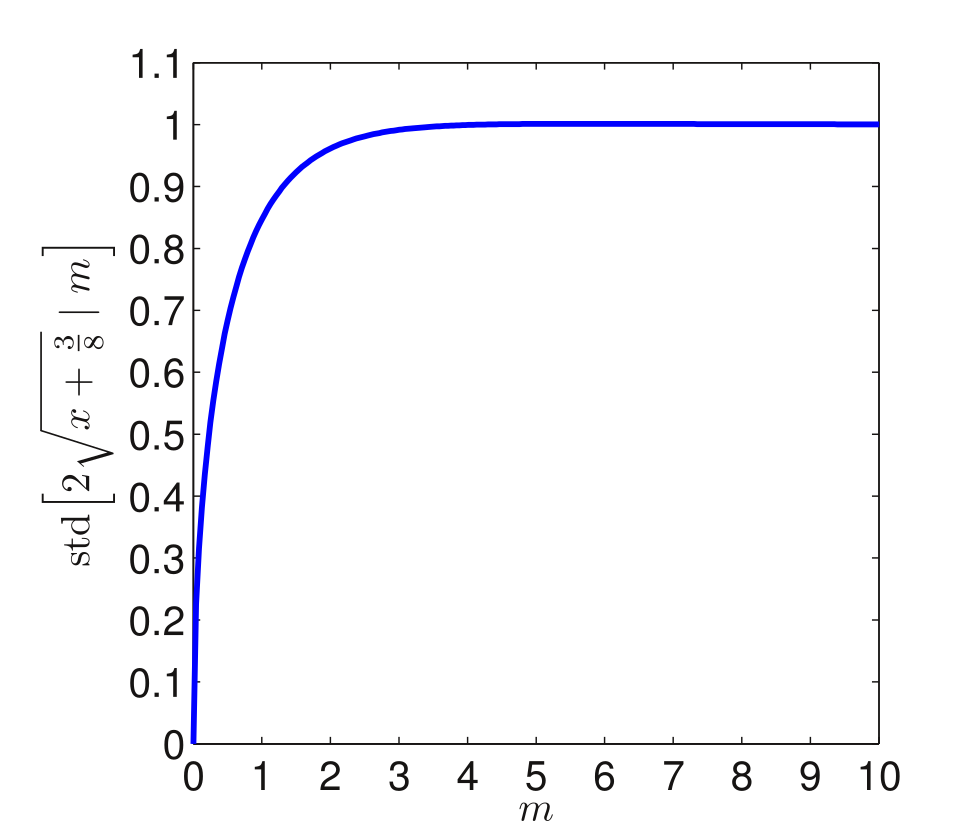
可见该变换利用了根号运算的特点,即在x较大时,y的值不再发生很大的变动,因此方差得到一定程度的稳定:
参考文献
[1] Wikipedia, https://en.wikipedia.org/wiki/Shot_noise.
[2] F. J. ANSCOMBE, THE TRANSFORMATION OF POISSON, BINOMIAL AND NEGATIVE-BINOMIAL DATA, Biometrika, Volume 35, Issue 3-4, December 1948, Pages 246–254.



