定义
期望最大化算法,简称EM算法,是统计学中通过不断迭代得到模型中参数的最大似然或最大后验概率的方法,其中模型依赖于未观测的隐藏变量。EM算法最早由Arthur Dempster、Nan Laird和Donald Rubin在1977年的一篇经典论文中解释和命名的。他们指出,该方法已经被早期的作者“在特殊情况下多次提出”[1]。
EM是一种解决存在隐含变量优化问题的有效方法,其经过E step与M step两步进行迭代计算。其中E step用于计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;M step则是最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一次E步计算中,这个过程不断交替进行。
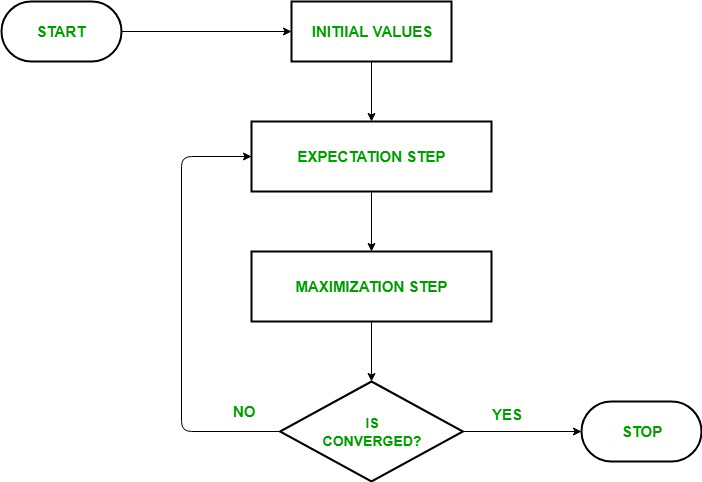
图 1 EM算法流程图[2]
参考文献
[1] Dempster, A.P.; Laird, N.M.; Rubin, D.B. (1977). "Maximum Likelihood from Incomplete Data via the EM Algorithm". Journal of the Royal Statistical Society, Series B. 39 (1): 1–38. JSTOR 2984875. MR 0501537.
[2] https://www.geeksforgeeks.org/ml-expectation-maximization-algorithm/



