定义
信号功率谱对数值进行傅里叶逆变换的结果,即信号→功率谱→对数→傅里叶逆变换。
倒频谱变换是频域信号的傅立叶积分变换的再变换。时域信号经过傅立叶积分变换可转换为频率函数或功率谱密度函数,如果频谱图上呈现出复杂的周期结构而难以分辨时,对功率谱密度取对数再进行一次傅立叶积分变换,可以使周期结构呈便于识别的谱线形式。第二次傅立叶变换的平方就是倒功率谱,即“对数功率谱的功率谱”。倒功率谱的开方即称幅值倒频谱,简称倒频谱。
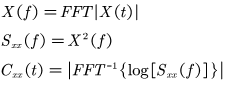
其中,![]() 是时域振动信号,
是时域振动信号,![]() 是时域振动信号的功率谱,
是时域振动信号的功率谱,![]() 是时域振动信号的倒频谱。
是时域振动信号的倒频谱。
倒谱的理解
频谱(功率谱)反应频率特征点的横坐标是频率f(Hz),而在倒频谱中对应的特征点的横坐标是时间t(s),而f与t互为倒数。从这里也可以看出,虽然倒频谱也叫“频谱”,其横坐标却并不是频率,而是时间。
倒谱的意义
方便提取、分析原频谱图上肉眼难以识别的周期性信号:
倒频谱能很好地检出功率谱上的周期成分,通常在功率谱上无法对边频的总体水平做出定量估计,而倒频谱对边频成分具有概括能力,能较明显地显示出功率谱上的周期成分,将原来谱上成族的边频带谱线简化为单根谱线,而齿轮发生故障时的振动频谱具有的边频带一般都具有等间隔(故障频率)的结构,利用倒频谱这个优点,可以检测出功率谱中难以辨识的周期性信号。
受传感器的测点位置及传输途径的影响小:
对于布置在不同位置的传感器,由于传递路径不同,其功率谱也不相同。但在倒频谱上,由于信号源的振动效应和传递途径的效应分离开来,代表齿轮振动特征的倒频率分量几乎完全相同,只是低倒频率段存在由于传递函数差异而产生的影响。在进行倒频谱分析时,可以不必考虑信号测取时的衰减和标定系数所带来的影响。这一优点对于故障识别极为有用。
参考文献
[1] 频域特征值提取的MATLAB代码实现(频谱、功率谱、倒频谱) - Mr.括号的文章 - 知乎https://zhuanlan.zhihu.com/p/36163931
[2] 倒频谱原理与Python实现,https://www.cnblogs.com/RoseVorchid/p/12012822.html
参阅:功率谱、傅里叶变换、功率谱密度



