定义
霍夫曼编码 (Huffman Coding)，是一种不唯一的不定长的无损信息压缩编码方式。
霍夫曼编码 (Huffman Coding)又称哈夫曼编码，有时称之为最佳编码。霍夫曼编码是不定长编码，即代表各元素的码字长度不等。该方法完全依据字符出现概率来构造平均长度最短的码字。该编码是基于不同符号的概率分布，在信息源中出现概率越大的符号相应的码越短，出现概率越小的符号其码越长，从而达到利用尽可能少的符号表示源数据。
1952年，David A. Huffman在麻省理工攻读博士时发表了《A Method for the Construction of Minimum-Redundancy Codes》，从此后世称之为Huffman编码。Huffman受到了香农（Shannon）和范若（Fano）的启发创造出了基于概率的编码。其基本方法是先对图像数据扫描一遍，计算出各种像素出现的概率，按概率的大小指定不同长度的唯一码字，由此得到一张该图像的霍夫曼码表。
生成霍夫曼编码算法基于一种称为“编码树”（coding tree）的技术。算法步骤如下：
（1）初始化，根据符号概率的大小按由大到小顺序对符号进行排序。
（2）把概率最小的两个符号组成一个新符号（节点），即新符号的概率等于这两个符号概率之和。
（3）重复第2步，直到形成一个符号为止（树），其概率最后等于1。
（4）从编码树的根开始回溯到原始的符号，并将每一下分枝赋值为1，上分枝赋值为0。
具体操作上，现假设信息源空间 为
其中
，先用r个码的号码集
对信源A中的每一个符号ak进行编码。编码过程如下：
（1）把信源符号ai按其出现的概率的大小顺序排列起来；
（2）把最末两个具有最小概的元素之概率加起来；
（3）把该概率之和同其余概率由大到小排队，然后再把两个最小概率加起来，再排队；
（4）重复步骤(2)、(3)，直到概率和达到1为止；
（5）在每次合并消息时，将被合并的消息赋以1和0或0和1；
（6）寻找从每个信源符号到1处的路径，记录下路径上的1和0；
（7）对每个符号写出"1" "0"序列(从码数的根到终节点) 从而创建霍夫曼表；
（8）压缩编码时，将码值用码字代替。
具体构造和编码实例如下图所示：
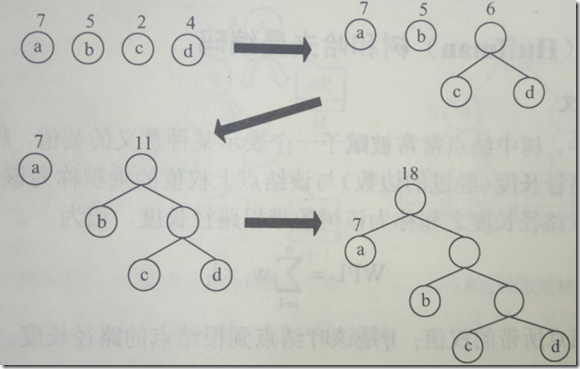
霍夫曼编码的特点：
- 霍夫曼方法构造出来的码不是唯一的；
- 编码码字字长参差不齐；
- 霍夫曼编码对不同的信源的编码效率是不同的。当信源概率相等时,其编码效率最低。只有在概率分布很不均匀时，霍夫曼编码才会收到显著的效果；
- 解码时,必须参照霍夫曼编码表才能正确译码；
- 霍夫曼编码是一种统计编码，属于无损压缩编码；
- 广泛用于JPEG，MPEG等各种信息编码。
参考文献
[1] Huffman D A . A method for the construction of minimum-redundancy codes[J]. Resonance, 2006, 11(2):91-99.
[2] 徐佳迪.霍夫曼编码及其效率的研究[D].江苏：南京林业大学电子信息工程学院，2012
[3] Katona G, Nemetz T. Huffman Codes And Self-information[M]. 1976.
[4] Andrzej Siemiński. Fast decoding of the Huffman codes[J]. Information Processing Letters, 26(5):237-241.
参阅：信号压缩、压缩编码、稀疏域变换
