快速傅里叶变换原理
在一维的傅里叶变换中,算法的复杂度是O(N2),而在快速傅里叶变换中,算法的复杂度为O(Nlog2N),因此快速傅里叶变换能够实现更快的计算速度。
快速傅里叶变换基于逐次加倍的方法,其中原始的一维傅里叶变换公式(1)能够写成两个递推的公式(2)、(3):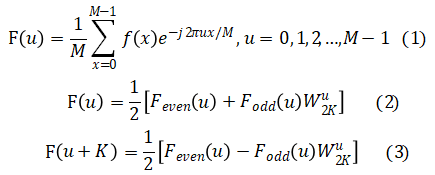
其中M=2n=2K,![]() ,且
,且

从递推公式来看,其实快速傅里叶变换的工作原理是,将一个M点的变换分成两个部分来计算,其中奇部和偶部的和能得到F(u)的前M/2个值,而奇部和偶部的差能得到F(u)的后M/2个值。换句话说,对于任意M=2n的离散傅里叶变换计算,可以通过计算M/2个点的值,来计算M个点的DFT,最后从2个单点的DFT出发,递推得到4个单点的DFT、8个单点的DFT,直到M个点的DFT。而二维的傅里叶变换可由连续2次一维傅里叶变换得到。
快速傅里叶变换的代码实现
快速傅里叶变换的算法主要分成两步:
(1)根据M个点的顺序的二进制值进行按位倒序。举个例子,在8点的快速傅里叶变换中,f(1)的顺序是1,原地址写成二进制是001,按照按位倒序,倒序后的新地址值是100,写成十进制是4,即在顺序1号位应该放置f(4)。这种做法其实是完成多次奇偶分组后的结果,将0作为偶分组,1作为奇分组。
(2)蝶形运算。以8点计算来说,蝶形运算如图1所示:
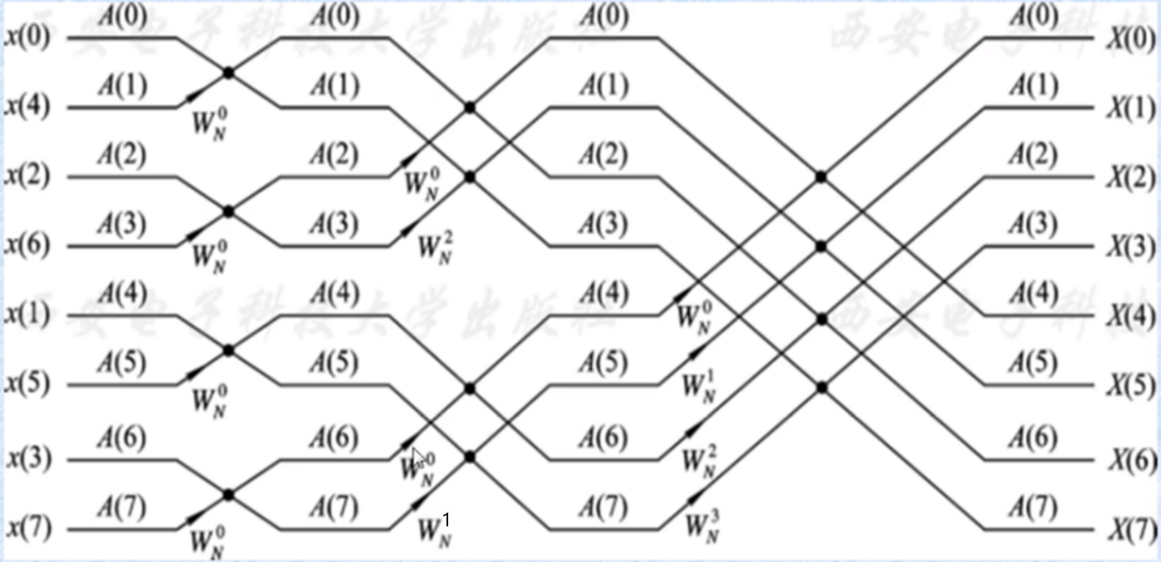
图 1 蝶形运算的图示
其中,在每一次计算后,蝶形运算时的地址增量是2n,其中M=2n+1.
具体的代码实现如图2所示:

图 2 快速傅里叶变换具体步骤的代码实现
而傅里叶逆变换的过程,实际上是在频域中取了共轭之后,再进行快速傅里叶变换并最后除以总点数,即完成傅里叶的逆变换。



