定义
峭度K是反映随机变量分布特征的数值统计量,是归一化4阶中心矩。
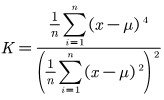
峭度是对实值随机变量的概率分布相对于正态分布而言是重尾还是轻尾的一种度量,即峭度高的数据集往往具有较重的尾(离群值);峭度低的数据集往往具有较轻的尾部(缺乏离群值),均匀分布是最极端的情况。
与偏度类似,峭度也是描述了概率分布的形状(数据集的位置和变异度),二者不同在于,偏度本质上衡量的是分布的对称性,而峭度确定分布尾部的沉重度。
峭度的意义
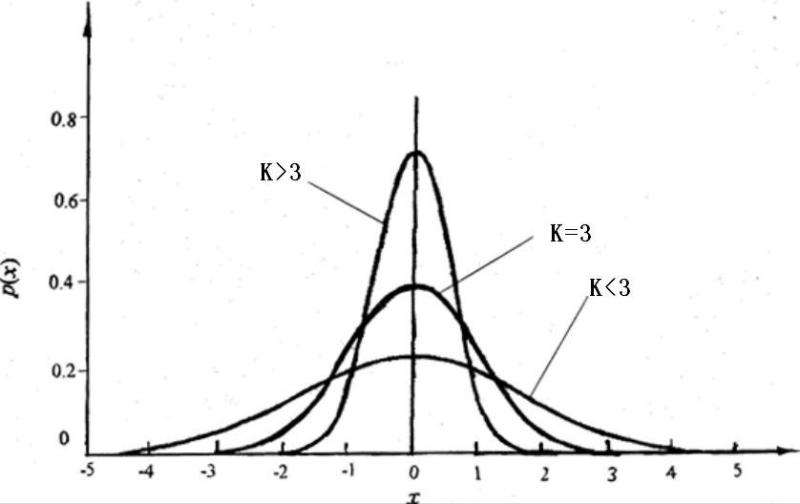
对于正态分布,峭度等于3;当K>3时,分布曲线具有正峭度。由此可知,当标准差小于正常状态下的标准差,即观测值的分散程度较小时,K增大,此时正态分布曲线峰顶的高度高于正常正态分布曲线,故称为正峭度。正峭度分布曲线两侧有较重的尾部,表存在较大的离群值。当K<3时,分布曲线具有负峭度,当标准差大于正常状态下的标准差,即观测值的分散程度较大时,K减小,此时正态分布曲线峰顶的高度低于正常正态分布曲线,故称为负峭度。负峭度分布曲线尾部较平,表明分布中的异常值较小。
峭度的应用
峭度指标是无量纲参数,由于它与轴承转速、尺寸、载荷等无关,对冲击信号特别敏感,特别适用于表面损伤类故障、尤其是早期故障的诊断。
在轴承无故障运转时,由于各种不确定因素的影响,振动信号的幅值分布接近正态分布,峭度指标值K≈3;随着故障的出现和发展,振动信号中大幅值的概率密度增加。信号幅值的分布偏离正态分布,正态曲线出现偏斜或分散,峭度值也随之增大。峭度指标的绝对值越大,说明轴承偏离其正常状态,故障越严重,如当其K>8时,则很可能出现了较大的故障。
在金融业中,峭度被用来衡量金融风险。峭度过大与投资风险高有关,因为这表明存在很高的极大和极小回报率的可能性。另一方面,小的峭度表示中等风险,因为极端收益的可能性相对较低。
参考文献
[1] https://corporatefinanceinstitute.com/resources/knowledge/other/kurtosis/
[2] https://en.wikipedia.org/wiki/Kurtosis
参阅:偏度、统计学、概率分布



