定义
各向异性扩散变分去噪方法。
Perona-Malik(P-M)方程是一种各向异性的变分去噪方法。变分图像去噪方法可按照方程的构造方法分为两类,一类是以TV方程为代表的构造能量泛函的方法,另一类是以P-M方程为代表的构造微分方程(PDE)的方法。
基于PDE的方法是根据演化时间t展开了一组图像。随着时间t的增加,原图像![]() 的估计
的估计![]() 越来越光滑。而且,在把图像
越来越光滑。而且,在把图像![]() 变得更光滑的同时还要保留原图中诸如边缘、角点这样的特征。热传导方程是最早在图像处理上应用的微分方程。
变得更光滑的同时还要保留原图中诸如边缘、角点这样的特征。热传导方程是最早在图像处理上应用的微分方程。
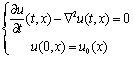
其中![]() 是图像的拉普拉斯算子。热传导方程的解可以一个使用高斯核与图像做卷积的过程。
是图像的拉普拉斯算子。热传导方程的解可以一个使用高斯核与图像做卷积的过程。
![]()
其中![]() 是均值为0,方差为
是均值为0,方差为![]() 的二维高斯核。利用热传导方程对图像进行处理与我们传统的高斯滤波的方法对图像处理具有同样的效果,也就是一个低通滤波器的效果。所以这种处理结果不加区别地去除了大量高频细节,使得图像边界非常模糊。
的二维高斯核。利用热传导方程对图像进行处理与我们传统的高斯滤波的方法对图像处理具有同样的效果,也就是一个低通滤波器的效果。所以这种处理结果不加区别地去除了大量高频细节,使得图像边界非常模糊。
为了克服热传导方程的缺点,在去除噪声的同时保护边缘,Perona和Malik提出了P-M方程。
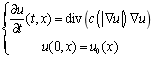
将热传导方程中的![]() 用图像梯度
用图像梯度![]() 的函数c替代。热传导方程就是
的函数c替代。热传导方程就是![]() 时的特殊情形。这里的c与TV方程中的φ是有些类似的,根据图像梯度的不同扩散程度也不同,不再是各向同性的了。最终需要达到这样的效果:
时的特殊情形。这里的c与TV方程中的φ是有些类似的,根据图像梯度的不同扩散程度也不同,不再是各向同性的了。最终需要达到这样的效果:![]() 较小的平滑区域会变得更加平滑;
较小的平滑区域会变得更加平滑;![]() 较大的边缘比较丰富的区域。既能去噪又能保持边缘的清晰。
较大的边缘比较丰富的区域。既能去噪又能保持边缘的清晰。
通常c会使用两种形式:![]() 和
和![]() 。这两种形式都有一个阈值K,用来区分图像的平坦区域和边缘区域。在
。这两种形式都有一个阈值K,用来区分图像的平坦区域和边缘区域。在![]() 的平坦区域
的平坦区域![]() ,与热传导方程一样,随着演化的进行一直在平滑。但在边缘附近梯度值大到
,与热传导方程一样,随着演化的进行一直在平滑。但在边缘附近梯度值大到![]() 后,
后,![]() ,演化变成了一个反向的过程,“回退”到了平滑之前,这就达到了增强边缘的效果。
,演化变成了一个反向的过程,“回退”到了平滑之前,这就达到了增强边缘的效果。
P-M方程的处理结果明显要好于用各向同性热传导方程的效果。可以保持纹理的边缘。当然P-M方程也有缺陷,与TV方程类似,处理后会产生很明显的分块的区域,与周围图像灰度的过渡很不自然。针对这一问题后来又有很多改进方法,比如使用了更高阶的偏微分方程克服这种阶梯效应等。
参考文献
[1] Koenderink J J. The structure of images[J]. Biological cybernetics, 1984, 50(5): 363-370
[2] Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE Transactions on pattern analysis and machine intelligence, 1990, 12(7): 629-639.
[3] Guidotti P. Some anisotropic diffusions[J]. Ulmer Seminare, 2009, 14: 215-221.
参阅:变分法、偏微分方程、热传导方程、TV方程



