定义
降维是模式识别、机器学习、计算机视觉等领域的重要研究课题。从实际中获得的数据往往呈现出多元性和非线性。拉普拉斯降维(Laplacian Eigenmaps)是一种常见的非线性降维方法，主要思想是采用图的拉普拉斯算子描述流形的局部特征，求解能够保持数据之间远近关系的低维嵌入[1]。
拉普拉斯特征映射方法采用图的拉普拉斯算子来描述流形的局部结构特征，具体步骤如下：1）构造局部领域图，通常采用KNN-近邻或者ε近邻；2）选择合理的方式设定领域图边权重系数
，
表示i的领域点的下标集合；3）通过矩阵谱分解获得高维数据的低维表示。
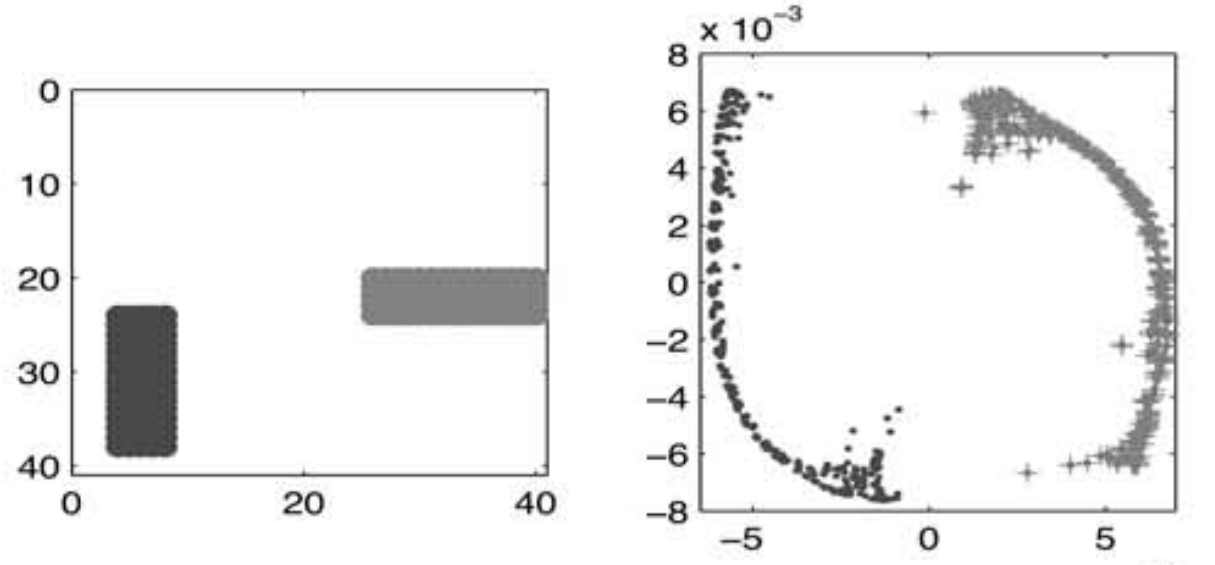
图 1 (a)两类原始数据，(b)LE降维后的数据[2]
参考文献
[1] Zhou, Honghu, and Jun Wang. "Laplacian Eigenmaps Dimensionality Reduction Based on Clustering-Adjusted Similarity." Algorithms 12.10 (2019): 210.
[2] Belkin, Mikhail, and Partha Niyogi. "Laplacian eigenmaps and spectral techniques for embedding and clustering." Advances in neural information processing systems. 2002.
