概述
Brier分数Glenn W. Brier在1950年提出。作为一种评分函数,brier分数多用于衡量概率预测的准确性。具体而言,多用于评估分类任务中模型预测结果的准确性。
Brier分数的计算公式如下:
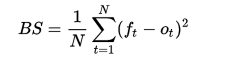
其中N代表所有预测事件的数目,ft是预测事件发生的概率,ot是事件真实发生的情况,ot=1代表该预测结果发生,反之ot=0则说明该事件并未发生。通过计算两者之间差距的平方和为预测结果进行评估。实际上,该分数是预测的均方误差。这个公式主要用于二分类事件。如果要对多类别预测进行评价,则应使用如下所示的原始定义。

其中R代表预测事件的类别,Brier评分越低代表预测概率与真实事件之间的差异越小,概率预测越准确。
对于非常罕见(或非常频繁)的事件,Brier评分变得不够充分,因为它不能充分区分预测中对罕见事件具有重要意义的微小变化。Wilks 曾指出 “对相对罕见的事件进行预测需要大样本容量,即n > 1000,而对普通事件进行预测只需要相当小的样本容量。”
参考文献
[1] Brier G W. Verification of forecasts expressed in terms of probability[J]. Monthly weather review, 1950, 78(1): 1-3.
[2] https://en.wikipedia.org/wiki/Brier_score
[3] Benedetti R. Scoring rules for forecast verification[J]. Monthly Weather Review, 2010, 138(1): 203-211.
[4] Wilks D S. Sampling distributions of the Brier score and Brier skill score under serial dependence[J]. Quarterly Journal of the Royal Meteorological Society, 2010, 136(653): 2109-2118.



