定义
I/Q数据显示了正弦波的幅度和相位的变化。
简单地说,I/Q数据显示了正弦波的幅度和相位的变化。如果振幅和相位变化以人为设定的方式有序地发生,我们可以利用振幅和相位变化将信息编码到正弦波上,这个过程称为调制。
调制过程是将包含信息的低频信号载入到高频载波信号中。I/Q数据在射频通信系统中非常普遍,在信号调制中更为普遍,因为它是一种方便的信号调制方式。
什么是信号(signal)?
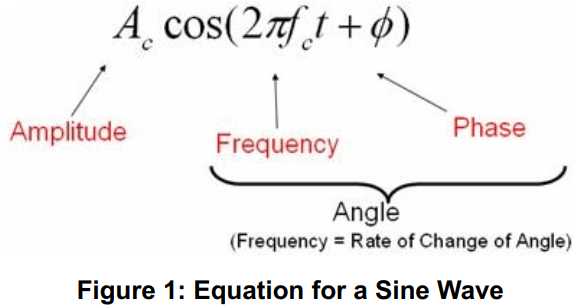
信号调制即改变一个正弦波来编码信息。表示正弦波的方程如下:
上面的等式表明,我们只能通过改变正弦波的振幅、频率和相位来对信息进行编码。频率就是一个正弦波的相位变化率(频率是相位的一阶导数),所以正弦波方程的频率和相位可以统称为相位角。因此,在振幅和相位构成的极坐标系中,正弦波的瞬时状态可以用该极坐标系中复平面上的一个矢量来表示。
在上图中,从原点到黑点的距离代表了正弦波的振幅,从横轴到直线的角度代表了相位。因此,只要正弦波的振幅不变(调制),从原点到点的距离就不变。点的相位根据正弦波的状态而变化。例如,一个正弦波的频率为1赫兹(以每秒一转的速度绕原点逆时针旋转)。如果振幅在一次旋转中没有改变,圆点就会在原点周围画出一个半径等于振幅的圆,圆点在原点上的移动速度为每秒一个周期。
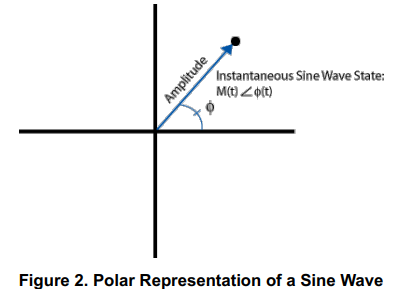
因为相位是一种相对测量,假设所使用的相位基准是某个频率的正弦波。当参考正弦波频率与标绘的正弦波频率相同时,两信号相位的变化率相同,正弦波绕原点的旋转是静止的。在这种情况下,一个振幅/相位点可以代表一个频率等于参考频率的正弦波。在原点周围的任何相位旋转都表示参考正弦波和正在绘制的正弦波之间的频率差。
到目前为止,我们已经描述了极坐标系统中的振幅和相位数据。上面讨论的所有概念都适用于I/Q数据。事实上,I/Q数据只是将振幅和相位数据从极坐标系统转换为笛卡尔(X,Y)坐标系统。利用三角函数,你可以把极坐标的正弦波信息转换成直角坐标系的I/Q正弦波数据。这两种表示是等价的,包含相同的信息,只是形式不同。这种等价性如图3所示。
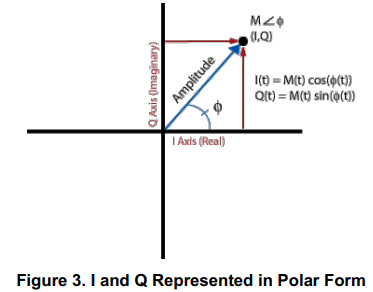
下图展示了一个LabVIEW示例,演示了极坐标和笛卡尔坐标之间的关系。
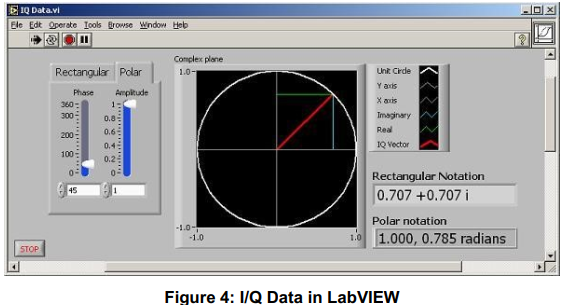
通信系统中的I/Q数据
要解释为什么I/Q数据用于通信系统,我们必须了解调制基础。
射频通信系统使用调制的方式来增加在一定频谱范围内可以传输的数据量。信号调制可分为两大类:模拟调制和数字调制。模拟或数字指的是如何调制数据。如果将模拟音频数据调制到载波正弦波上,这种技术称为模拟调制。如果模拟音频数据由模数转换器(ADC)采样,并将产生的数字位调制到载波正弦波上,这种技术被定义为数字调制。模拟调制和数字调制都涉及到根据消息数据改变载波的振幅、频率或相位(或同时改变振幅和相位的组合)。
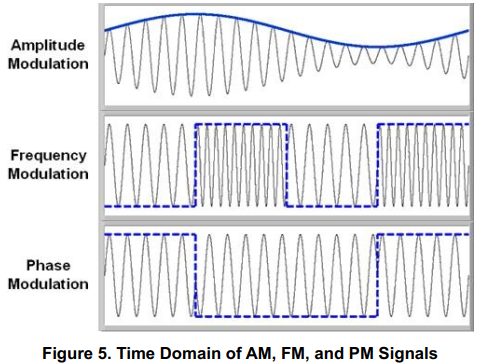
振幅调制(AM)、频率调制(FM)或相位调制(PM)都是模拟调制的例子。通过振幅调制,载波正弦波的振幅根据信息信号进行调制。同样的想法也适用于频率和相位调制。图5表示了AM、FM和PM的区别。对于AM来说,消息信号是蓝色的正弦波,它构成了高频载波正弦波的“包络线”。对于FM,消息数据是虚线方波。如图所示,产生的载波信号在两个不同的频率状态之间变化。每个频率状态表示消息信号的高状态和低状态。在这种情况下,如果消息信号是一个正弦波,频率会有一个更平缓的变化,这将更难观察到。对于PM,请注意虚线方波消息信号边缘的明显相位变化。
如前所述,如果载波正弦波振幅变化对时间(消息信号)成正比,正如AM调制的情况一样, I/Q平面图形只改变从原点到I/Q点的距离,如下图所示:

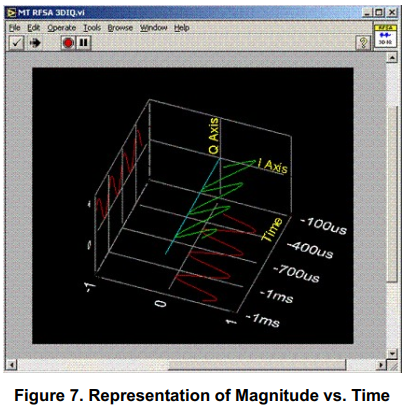
上图显示的是I/Q数据点的振幅变化,相位固定在45度。我们并不知道信息信号,只能知道它是调幅的。但是,如果观察到I/Q数据点的幅度随时间的变化,基本上就可以看到消息信号的表示形式。利用LabVIEW的三维图形控制,我们可以显示时间的第三轴来说明消息信号。
信号轨迹的幅度以正弦模式调制,表明消息信号是一个正弦波。绿色的轨迹表示在极坐标系统中的振幅和相位数据,而红色的轨迹表示波形在I和Q轴上的投影,表示单独的I和Q波形。我们可以使用PM显示相同类型的示例,如下图所示:
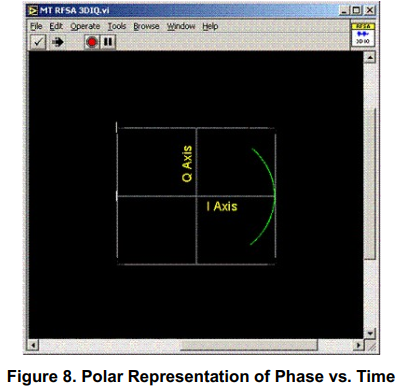
可以看出消息信号是相位调制的,因为振幅是恒定的,但是相位在变化(调制)。我们无法看到消息信号相对于时间的形状,但是可以看到消息信号的最小和最大信号级别分别由-45度和+45度的相位偏差表示。加入时间轴可以用来更好地理解这个概念,如下图所示:
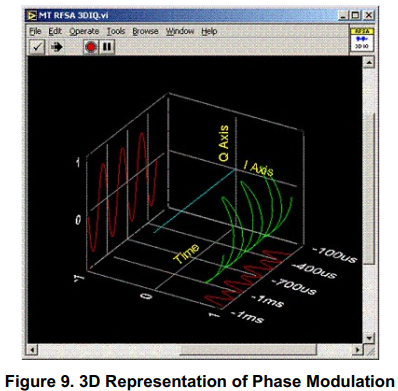
在LabVIEW 3D图形中显示的图9中,绿色轨迹随时间呈正弦变化。在I轴和Q轴上的投影示与具有固定大小和振荡相位的PM正弦波对应的单个I和Q波。本质上,I/Q数据表示消息信号。因为I/Q数据波形是极坐标系振幅和相位波形的笛卡尔坐标系的投影,所以可能很难确定消息信号的性质。例如,将图9中的红色I和Q波形与图9中的绿色波形进行比较。如果你绘制AM信号的振幅与时间的关系,你会看到消息信号。如果你画出AM信号的相位数据和时间关系,你会得到一条直线。这对于同时调制振幅和相位的更复杂的数字调制方案来说并不一定是这样。
那么为什么要使用I/Q数据呢?
因为振幅和相位数据看起来更直观,你可以假设你应该使用极坐标振幅和相位数据,而不是笛卡尔坐标I和Q数据。但是,考虑到实际的硬件设计,I和Q数据是更好的选择。
在硬件电路中,根据输入信息信号精确地改变高频载波正弦波的相位是很困难的。因此,控制载波正弦波振幅和相位的硬件信号调制器价格昂贵,设计和制造起来也很困难,而且结果证明,它不如使用I和Q波形的电路灵活。要了解如何避免直接操纵射频载波的相位,请参考以下I/Q调制方程:

注意,相同频率的正弦波和余弦波之间的相位差是90度。本质上,这个事实意味着你可以通过简单地分别控制I和Q输入信号的振幅来控制调制信号的振幅、频率和相位。用这种方法,你不需要直接改变射频载波正弦波的相位。你可以通过控制输入I和Q信号的振幅来达到同样的效果。当然,方程的后一半是一个正弦波,前一半是一个余弦波, 因此,必须在硬件电路中添加一个设备,以在I和Q混频器使用的载波信号之间产生90度相移,但是这个附加的设计问题比前面提到的直接相位操作要简单。
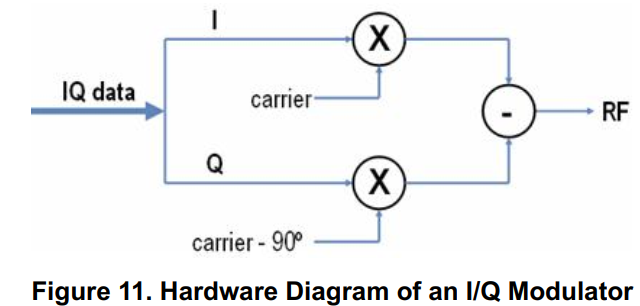
I/Q调制器将I波形与射频载波正弦波混频,并将Q信号与相同射频载波正弦波的90度相移混频。从I信号中减去Q信号(正如图10中第3行所示),就得到最终的RF调制波形。实际上,载波的90度偏移是I和Q数据名称的来源,I表示同相位数据(因为载波在相位中),Q表示正交数据(因为载波偏移了90度)。这种技术被称为正交上转换,您可以对任何调制方案使用相同的I/Q调制器。I/Q调制器只是对I和Q波形振幅的变化作出反应,而I和Q数据可以表示消息信号的幅度和相位的任何变化。I/Q调制器设计的灵活性和简单性(相对于其他选项)是它如此广泛使用和流行的原因。
参考文献
[1] https://search.ni.com/nisearch/app/main/p/bot/no/ap/tech/lang/zhs/pg/1/ps/20/sn/catnav:tu/scope/zh-CN/
参阅:幅度调制、频率调制、相位调制



