RANSAC英文全称为random sample consensus,中文译为随机抽样一致。RANSAC可以通过迭代的方式从一组包含离群值的观察样本中估计出特定数学模型的参数,也可以作为一种离群值检测的方法。
RANSAC算法的基本假设如下:
1、样本数据由内群数据(inliers)和外群数据(outliers)组成。内群数据可以用于模型参数的估计;而外群数据是对模型的估计没有价值的异常值,可能由错误的测量结果导致。
2、给定一组内群数据,存在一个过程可以估算出该组数据最适合的模型参数。
为了更好地阐述RASAC的算法思路,本文借鉴了wiki的介绍实例:二维直线拟合[1],如下图1所示。在该实例中,数据点中包含内群点和外群点,预期目标是排除外群数据点的干扰,仅实现内群数据点的直线拟合。
算法思路如下:
1、随机选取两个点作为内群点;
2、计算这两点连接线的斜率k和截距b,作为直线的模型参数M;
3、遍历计算其余所有点与该直线的距离,如果小于阈值d,则认为该点属于内群点;
4、遍历完所有点后,记录此时内群点的个数n;
5、重复步骤1-4,k次;
6、选取内群点个数最多时对应模型参数M,作为整体数据的直线模型参数。
不难看出,只要将步骤2中对直线模型M的估计换成其余数学模型参数的估计,该算法便可以广泛地适用。
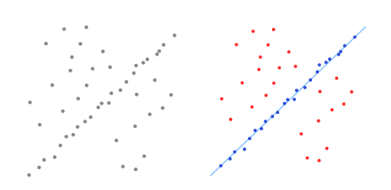
图 1 利用RANSAC实现二维直线拟合的示意图。左图为所有的数据点,右图中蓝色点为算法识别的内群点,蓝色直线为对应的拟合直线,红色点为外群点。
RANSAC算法优点是鲁棒性好,即便存在较多的外群点也可以实现数学参数的模型估计。缺点是算法结果容易受到迭代次数k的影响,当k较小时往往难以得到最优的参数估计。此外,另一个比较明显的不足时,RANSAC算法只能从样本数据中估计出一个模型,如果样本数据存在两个及以上模型时,该算法并不适用。
参考文献
[1] https://en.wikipedia.org/wiki/Random_sample_consensus.



