定义
最近邻法(KNN算法,又称K-近邻算法)是一种用于分类和回归的非参数统计方法[1],在K-NN分类中,输入包含在特征空间中的K个最接近的训练样本,输出是一个分类族群;在K-NN回归中,输出是对象的属性值,该值是K个最近邻的取值的平均[2]。
主要原理
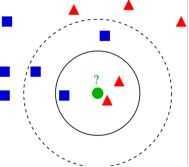
图 1 K-NN分类示意图
K-NN分类原理为:每个待分类点通过邻域点的多次投票来进行分类,待分类点被分配给其最接近的K个邻点中最常见的类别,其中K是一个参数,通过定义邻域中相邻点的数目来划定邻域的范围。
如上图所示,假设目前有两个类别,分别以蓝色和红色表示,需要将绿色点进行分类。如K=3,则邻域范围是实线圆圈内的区域,此范围内红色点数目多于蓝色点数目,因此绿色点被划分为红色类。如K=5,则被划分为蓝色类。
在实际应用中,距离度量一般采用欧氏距离。当无法判定当前待分类点是从属于已知分类中的哪一类时,可以依据统计学的理论看它所处的位置特征,而把它归为(或分配)到数目更多的那一类。
在KNN回归时,使用K个最近邻居的加权平均值作为输出,权重为距离的倒数。
首先,计算从待取值点到周围空间点的欧几里得距离或马氏距离,按照距离的大小,从近到远排列已知类别的空间点。基于交叉验证算法计算均方根误差,找到最佳的参数K值。最后,对K个近邻点取值进行距离反比加权,得到待取值点的预测数值。
模型的训练和预测
K 值的选择、距离度量和分类决策规则是KNN分类及回归的关键。下面以KNN分类为例展示训练和分类过程。
训练阶段:输入特征向量(特征参数)及类别标签,并进行存储。该算法的训练阶段仅包括存储训练样本的特征向量和类别标签。
分类阶段:K是用户定义的常数,未分配测试点通过找到最接近该点的K个训练样本中最频繁的标签进行分类。
K值的选择
K 值的选择会对算法的结果产生重大影响。K值较小意味着只有与输入实例较近的训练实例才会对预测结果起作用,但容易发生过拟合;如果 K 值较大,优点是可以减少学习的估计误差,但缺点是学习的近似误差增大,这时与输入实例较远的训练实例也会对预测起作用,使预测发生错误。在实际应用中,K 值一般选择一个较小的数值,通常采用交叉验证的方法来选择最优的 K 值[3]。
参考文献
[1] https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm
[2] Cover T, Hart P. Nearest neighbor pattern classification[J]. IEEE transactions on information theory, 1967, 13(1): 21-27.
[3] Campos G O, Zimek A, Sander J, et al. On the evaluation of unsupervised outlier detection: measures, datasets, and an empirical study[J]. Data Mining and Knowledge Discovery, 2016, 30(4): 891-927.



