定义
一种针对信息亚采样获取造成的欠定方程组求解稀疏域结果的方法。
压缩感知是基于待求信号在稀疏域的稀疏性,在远低于Nyquist采样频率的情况下,通过对信号的随机观测进行重建的方法。压缩感知理论最早在2005年由Donoho提出重建方法,在2006年由Candes和Tao论证了重建成功的RIP条件,由Baraniuk得出了RIP的等价条件是观测矩阵和稀疏基的不相关性。
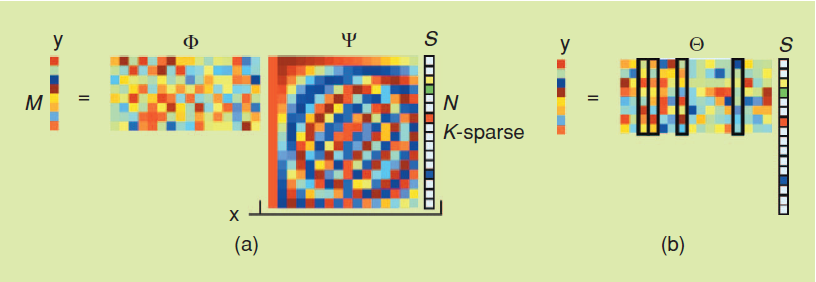
上图是一个有关压缩感知过程的简略示意图,x为长度为N的待求解的信号,Φ为设计好的观测矩阵,起到对待求解信号进行亚采样的效果,y为长度为M(M<N)的采集所得信号,S为信号x在稀疏域的变换(x=ψ*S),长度同样为N,稀疏度K定义为S中非零元素的个数。压缩感知的过程就是一个从采集得到的信号y复原原信号x的过程(y=Φ*x),虽然原方程是难以求解的欠定方程,但是当x可以表示为稀疏域中稀疏度为K的S时,相当于添加了K个条件(S中的K个分量为0),此时就可以通过特定算法求解。
压缩感知的本质就是利用了信号在特定变化下的稀疏度赋予方程新的条件从而求解。压缩感知的两大条件在于稀疏性和不相关性。若信号在某个域中只有少量非零值,那么它在该域稀疏,该域也被称为信号的稀疏域,因此信号必须在某一个领域拥有稀疏性,然而通常信号在变换域中不会呈现完全的稀疏性。其实只要它近似满足稀疏性,即大部分值趋于零,只有少量大的非零值,就可以认为它是可压缩信号,可以对它进行CS亚采样。而所谓的不相关性指压缩感知需要观测矩阵满足RIP条件(约束等距性条件),而后又证明RIP的等价条件是观测矩阵和稀疏表示基不相关。因此在满足稀疏性和不相关性两大条件之后方可完成压缩感知重建。
压缩感知理论包括信号的稀疏表示、观测矩阵的设计和信号重构算法三个部分。
信号的稀疏表示可以根据信号本身特点灵活选取,常用的稀疏基包括括离散余弦变换基、快速傅里叶变换基、离散小波变换基、Curvelet基、Gabor 基以及冗余字典等。
观测矩阵需要与稀疏表示基不相关,常见的观测矩阵包括随机高斯测量矩阵、随机伯努利测量矩阵、部分哈达玛测量矩阵、部分正交测量矩阵、稀疏随机测量矩阵、托普利兹和循环测量矩阵等。
重建算法的目的在于解决稀疏度条件下的原欠定方程组,即解决L0范数最小化问题,一种解决方案是利用贪婪算法的思想,依次从观测矩阵中选取与采样信号y的残差最匹配的列逼近,然后更新残差依次迭代。这种思想依次产生了MP(匹配追踪算法)、OMP(正交匹配追踪算法)、CoSaMP等具体的算法。
另一种解决方案是将L0范数最小化转化为L1范数最小化问题求解。还有诸如全变分最小化法、迭代阈值法、贝叶斯学习法等重建算法。
压缩感知的应用也很广泛,可作为图像处理手段进行图像复原与去噪、基于压缩感知技术的图像融合与压缩和图像超分辨、图像识别等,也可以作为成像手段改善核磁共振成像、CT成像速度,同时应用于雷达成像和单像素相机上,除此之外压缩感知也可以应用于信道编码、生物传感、数据通信、宽带接收机等等诸多领域。
参考文献
[1] Donoho, D. L. Compressed sensing. IEEE Transactions on Information Theory 52, 1289-1306, doi:10.1109/tit.2006.871582 (2006).
[2] Candes, E. J. & Tao, T. Near-Optimal Signal Recovery From Random Projections: Universal Encoding Strategies? IEEE Transactions on Information Theory 52, 5406-5425, doi:10.1109/tit.2006.885507 (2006).
[3] Tsaig, Y. & Donoho, D. L. Extensions of compressed sensing. Signal Processing 86, 549-571, doi:10.1016/j.sigpro.2005.05.029 (2006).
[4] Beck, A. & Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM Journal on Imaging Sciences 2, 183-202, doi:10.1137/080716542 (2009).
[5] Candes, E. J. & Tao, T. Near-Optimal Signal Recovery From Random Projections: Universal Encoding Strategies? IEEE Transactions on Information Theory 52, 5406-5425, doi:10.1109/tit.2006.885507 (2006).
参阅:稀疏表示、观测矩阵、OMP(正交匹配追踪算法)、RIP条件、单像素成像



