定义
采样定理，又称奈奎斯特采样定理（Nyquist Sampling），只要采样频率大于有效信号最高频率的两倍，采样值就可以包含原始信号的所有信息，被采样的信号就可以不失真地还原成原始信号。其中，采样频率是指单位时间内的采样点数。
数字信号处理领域，采样定理是连续时间信号（通常称为“模拟信号”）和离散时间信号（通常称为“数字信号”）之间的基本桥梁。该定理说明采样频率与信号频谱之间的关系，是连续信号离散化的基本依据。它为采样率建立了一个足够的条件，该采样率允许离散采样序列从有限带宽的连续时间信号中捕获所有信息。
需要指出，采样是一种周期性的操作， 非周期性采样不在采样定理的范围之内。
使用探测器进行数字成像的过程就对应于将实际的连续物理信号离散采样的过程，成像样本中最精细的结构在频域中相当于信号的最高频率，为了能够从获取的离散信号（以像素为单位记录的二维图像）恢复原来连续信号（实际成像样本）的全部信息，就需要满足物方采样间隔要小于物方能分辨最小细节尺寸的一半，可以表示为如下的形式：
其中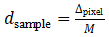
表示探测器最小面元
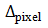在物方对应的采样间隔；
则表示物方能分辨最小细节尺寸，即系统设计的分辨率。
如果不能满足采样定理，采样后信号频率就会重叠，即高于采样频率一半的频率成分将被重建成低于采样频率一半的信号。这种频谱重叠导致的失真称为混叠，这种情况采集到的图像会失真，称为欠采样现象（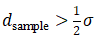
）。在实际应用中我们希望采样能够稍微“过”一点，即过采样，但是如果系统出现严重过采样的情况则说明系统的光学设计没能很好地实现器件间的匹配，过多的冗余造成浪费。
参考文献
[1] 姜建国, 曹建中, 高玉明. 信号与系统分析基础[M]. 2006.
[2] https://blog.csdn.net/qq_38405680/article/details/82748623
参阅：面阵相机、空间分辨率
