简介
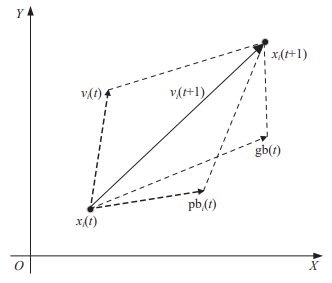
1995 年,Kennedy 和 Eberhart 两位博士[1] 共同 提出了粒子群优化算法 (Particle swarm optimization, PSO). ven den Bergh[2] 从理论角度对 PSO 算法的 稳定性和收敛性进行了分析和证明。2002 年,Cello 与 Lechuga[3] 正式发表了多目标粒子群优化算法的成果。粒子群算法求解多目标优化问题,称为多目标粒子群(Multiobjective particle swarm optimization, MOPSO)算法。PSO 算法中,将鸟群的个体位置或食物当作优化问题的解,利用群体中个体与最优个体以及个体之间的信息交互,引导整个群体中个体在保 留自身多样性信息的同时,朝向群体最优个体收敛,通过不断地更新逐渐找到最优解. 鸟群中个体被抽象为“粒子”,忽略其质量、体积,拓扑结构决定了每次迭代时“粒子”受到自身和群体状态信息 的综合影响,即粒子的更新机制是通过种群历史最优粒子和个体历史最优粒子的有机结合得到, 如图 1 所示。粒子 i 下一时刻的速度 是由当 前速度 、其自身最优位置 、全局最优位置 共同决定的,该粒子以更新后速度从当前位置移至新的位置 。随着迭代的不断深入,整个粒子群体在“引领者”的带动下,完成决策空间中最优解的搜索。
存在问题
多目标粒子群算法凭借其高效、快速的优势, 成为了多目标优化的主要研究方向。处理多目标优化问题时,既要克服传统多目标优化过程中的普遍性难点,又要考虑粒子群算法用于多目标优 化时的针对性问题,归纳如下:
优化过程中,如何挑选“领导”粒子,带领 整个种群在保留部分个体信息的前提下快速逼近 帕累托前沿,即最优粒子选择策略;
(1)粒子群算法中,种群个体受到“最优”粒子的影响,由于收敛过快而导致“早熟”,如何引导粒子“跳出”局部最优,即多样性保持机制;
(2)外部存储集中非支配解的数量的急剧增加,如何引导种群在保障多样性的前提下,进一步提高搜索效率,以强化算法在收敛速度方面的优势,即收敛性提高手段;
(3)如何在优化过程的不同阶段,动态协调整体开发和局部搜索之间的关系,以获得最佳优化结果,即多样性和收敛性的平衡方法;
(4)为了提升算法性能而进行的迭代公式的改进、重要参数的动态整定以及粒子间信息交互方式 的调整,即迭代公式、参数、拓扑结构的改进方案。
参考文献
[1] Kennedy J, Eberhart R. Particle swarm optimization//Proceeding of ICNN’95-IEEE International Conference on Neural Networks. Perth, 1995: 1942
[2] van den Bergh F. An Analysis of Particle Swarm Optimizers [Dissertation]. Pretoria: University of Pretoria, 2001
[3] Coello C A C, Lechuga M S. MOPSO: A proposal for multiple objective particle swarm optimization // Proceedings of the 2002 Congress on Evolutionary Computation. Honolulu, 2002: 1051
[4] 冯茜,李擎,全威,等. 多目标粒子群优化算法研究综述[J]. 工程科学学报,2021,43(6):745-753.



