概述
在数学(特别是功能分析)中,卷积是对两个函数(f和g)的数学运算,产生第三个函数,表示第一个函数的形状如何被另一个函数修改。术语卷积是指两个结果函数并计算它的过程。它定义为两个函数的乘积在一个函数被反转和移位后的积分。并针对所有shift值计算积分,从而产生卷积函数。
卷积的某些特征类似于互相关:对于实值函数,连续或离散变量,它与互相关的区别仅在于f(x)或g(x)围绕y轴反射; 因此,它是f(x)和g(-x)或f(-x)和g(x)的互相关。
卷积的应用包括概率,统计,计算机视觉,自然语言处理,图像和信号处理,工程和微分方程。
可以在欧几里得空间和其他组上的函数定义卷积。例如,周期函数,如离散时间傅立叶变换,可以在限定的圆和由卷积周期性卷积。可以为整数集上的函数定义离散卷积。
卷积的推广在数值分析和数值线性代数领域以及信号处理中的有限冲激响应滤波器的设计和实现中都有应用。计算卷积运算的逆数称为反卷积。
定义
f和g的卷积记为f ∗ g,用符号∗表示算符。[B]定义为其中一个函数反转和移位后两个函数乘积的积分。因此,这是一种特殊的整数转换:

等效的定义是:
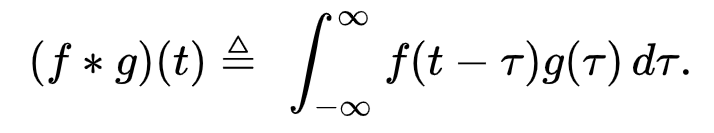
尽管上面使用了符号t,但它不一定代表时域。但是在这种情况下,卷积公式可以描述为在时刻t处函数f(τ)的加权平均值,其中权重由g(–τ)给出,只是移动了数量t。随着t的变化,加权函数会强调输入函数的不同部分。
对于仅在[0,∞)(即,对于负参数为零)上支持的函数f,g ,积分极限可以被截断,导致:

常见的工程惯例是[1]:
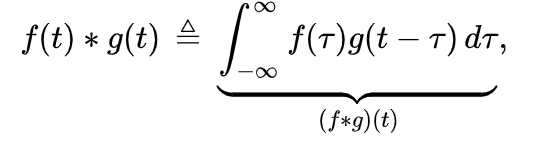
必须仔细解释以避免混淆。例如,f(t)* g(t – t 0)等于(f ∗ g)(t – t 0),但f(t – t 0)* g(t – t 0)实际上等效到(f ∗ g)(t − 2 t 0)[2]。
参考文献
[1] Smith, Stephen W (1997). “13.Convolution”. The Scientist and Engineer’s Guide to Digital Signal Processing (1 ed.). California Technical Publishing. ISBN 0-9660176-3-3. Retrieved 22 April 2016.
[2] Irwin, J. David (1997). “4.3”. The Industrial Electronics Handbook (1 ed.). Boca Raton, FL: CRC Press. p. 75. ISBN 0-8493-8343-9.
参阅:数字图像处理,信号与系统



